2025年05月04日成考高起点每日一练《数学(文史)》

2025年成考高起点每日一练《数学(文史)》5月4日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知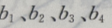成等差数列，且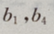为方程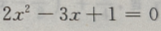的两个根，则的值为（）  

• A：
• B：
• C：
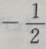
• D：

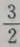
答 案：D

解 析：由根与系数的关系得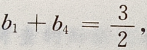由等差数列的性质得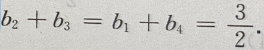

2、已知函数f（x）=5x+b，若f（-2）=3，则b=（）。

• A：3
• B：15
• C：7
• D：13

答 案：D

3、下列各式的值为零的是（）。

• A：0⁰
• B：log₁1
• C：
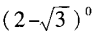
• D：log₂|-1|

答 案：D

解 析：0⁰和log₁1均没有意义，可排除（A）、（B），而（2-）⁰=1。故选D。

4、若A（-3，5），B（-5，-3），则线段AB中点的坐标为（）。  

• A：（4，-1）
• B：（-4，1）
• C：（-2，4）
• D：（-1，2）

答 案：B

主观题

1、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

2、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

3、已知F是椭圆的右焦点，点M在抛物线y2=2px（p＞0）上O为坐标原点，且△MOF为正三角形．  (Ⅰ)求P的值； (Ⅱ)求抛物线的焦点坐标和准线方程．

答 案：(Ⅰ)由椭圆方程可知，椭圆的长半轴a=5，短半轴，则椭圆的半焦距 即椭圆的右焦点F的坐标为 (4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点， 【考点指要】本题主要考查椭圆、抛物线的概念，要求考生掌握它们的标准方程和性质，会用它们解决有关的问题．  

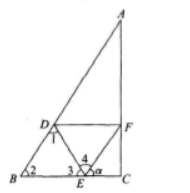
4、在△ABC中，已知AB=2,BC=1,CA=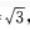 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 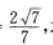求△DEF的边长。

答 案：解析:由AB=2，BC=1,CA=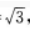 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα=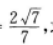 由此EC=lcosα 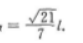有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

填空题

1、某学科的一次练习中，第一小组5个人成绩如下(单位：分)：98，89，70，92，90，则分数的样本方差为__________．

答 案：88．96

解 析：平均分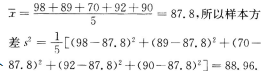 【考点指要】本题主要考查样本的平均数与方差的计算．对于统计问题，只需记清概念和公式，计算时不出错即可．  

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：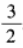

解 析：