2024年05月07日成考高起点每日一练《数学(文史)》

2024年成考高起点每日一练《数学(文史)》5月7日专为备考2024年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、函数y=x²+1（x＞0）的图像在（）

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：A

解 析：当x>0时，函数y=x²+1＞0，因此函数的图像在第一象限．

2、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

3、设M=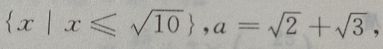那么（）

• A：
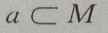
• B：
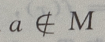
• C：
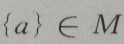
• D：

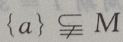
答 案：D

解 析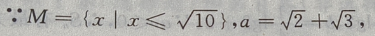： M是集合，a为元素，{a}为集合，元素与集合的关系是集合与集合的关系是  

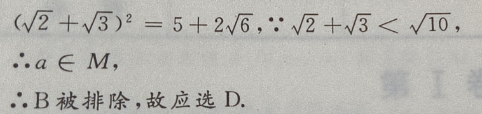
4、下列函数为奇函数的是 ( )。

• A：
• B：
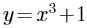
• C：
• D：

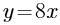
答 案：D

解 析：本题主要考查的知识点为函数的奇偶性．  【应试指导】f(z)=sinx=-sin(-x)=-f(-x)，所以y=sinx为奇函数．        

主观题

1、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

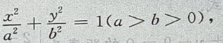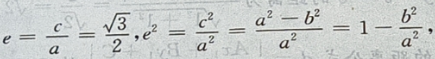
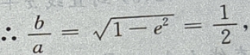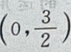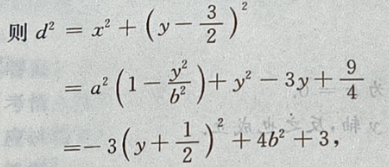
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 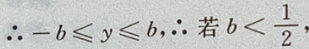则在y=-b时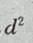，最大，即d也最大。  

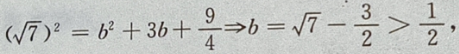
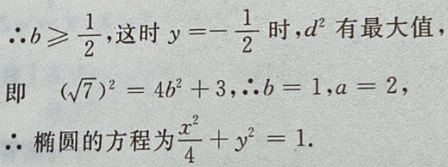
2、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图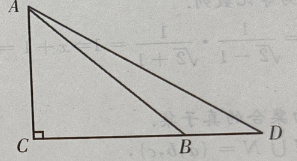  

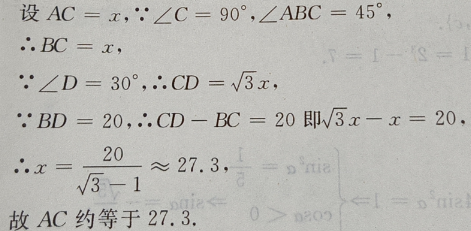
3、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

4、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.  

答 案：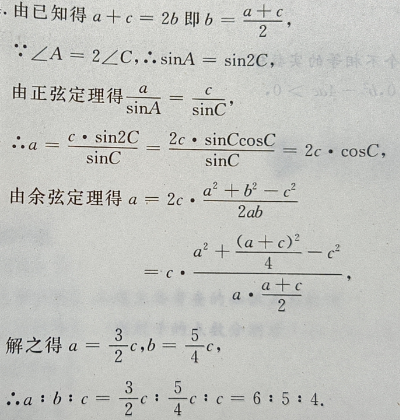

填空题

1、函数y=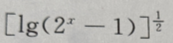的定义域是（）

答 案：[1,+∞)

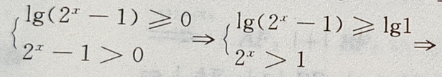
解 析：要是函数y=有意义，需使 所以函数的定义域为{x|x≥1}=[1,+∞)  

2、点（4,5)关于直线y=x的对称点的坐标为（）

答 案：(5,4)

解 析：点(4,5)关于直线y=x的对称点为（5,4).